how to find relative extrema using second derivative test

The Second Derivative Test is based on 2 prize-winning ideas: Showtime, that at the crest of a hill, a route has a hump shape — in other words, information technology's curving down or concave downward. And 2nd, at the bottom of a valley, a road is cup-shaped, so it's curving upwards or concave up.

The concavity of a function at a point is given by its 2nd derivative: A positive second derivative means the function is concave up, a negative second derivative means the role is concave down, and a 2d derivative of zero is inconclusive (the role could be concave up or concave down, or there could be an inflection bespeak there).

All local maximums and minimums on a part's graph — chosen local extrema of the function — must occur at critical points (where the first derivative is cipher or undefined). And then, to use the second derivative examination, you first have to compute the critical numbers, and so plug those numbers into the second derivative and notation whether your results are positive, negative, or nil.

Now analyze the post-obit function with the 2d derivative test:

Showtime, observe the first derivative of f, and since you lot'll need the second derivative after, you might as well detect information technology now equally well:

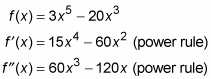
Side by side, fix the commencement derivative equal to zero and solve for x.

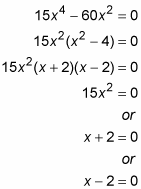
x = 0, –2, or ii.

These three ten-values are critical numbers of f. (Additional critical numbers could exist if the beginning derivative were undefined at some 10-values, but considering the derivative is a polynomial, information technology'south defined for all values of x.)

Now, plug the three critical numbers into the second derivative:

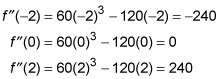
At –2, the 2nd derivative is negative (–240). This tells you that f is concave down where x equals –2, and therefore that there's a local max at –2. The second derivative is positive (240) where x is 2, so f is concave upwardly and thus there's a local min at x = 2. Because the second derivative equals zero at x = 0, the 2d Derivative Test fails — it tells you nothing about the concavity at x = 0 or whether there's a local min or max there. When this happens, y'all have to use the Showtime Derivative Test. In this instance, you find that at that place is neither a min nor a max at 10 = 0; at that place'southward an inflection point at that place.